Général
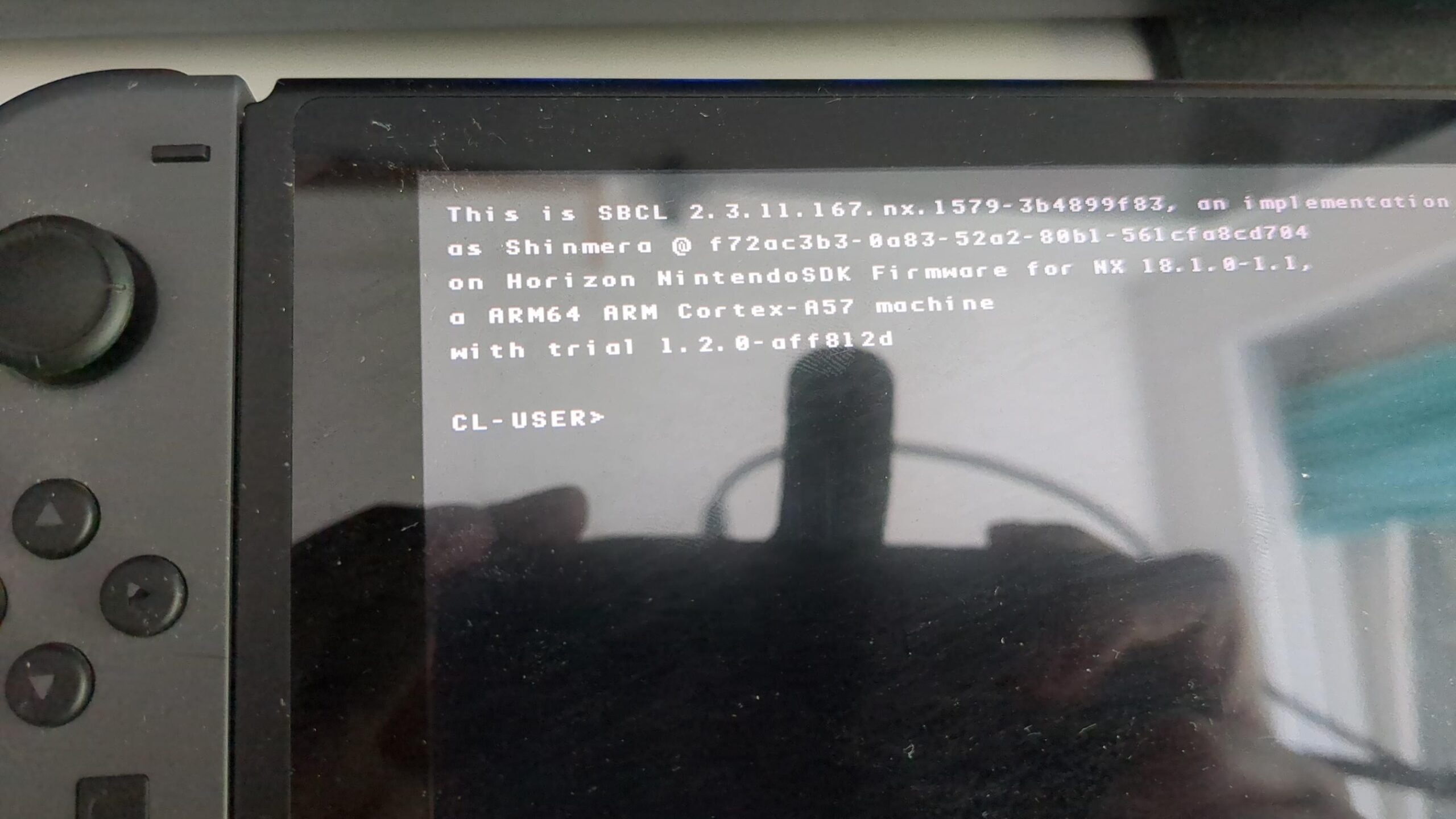
C99 est-il vraiment Turing-complet ? Découvrez-le !
La question de la complétude de Turing en C suscite de nombreux débats parmi les passionnés de programmation. Peut-on vraiment simuler une machine de Turing avec ce langage ? Bien que C offre une flexibilité impressionnante, il existe des limites inhérentes à sa structure. En effet, la gestion de la mémoire et des pointeurs impose des contraintes qui pourraient restreindre son expressivité. Découvrons ensemble pourquoi C pourrait ne pas atteindre cette fameuse complétude, et comment ses caractéristiques uniques façonnent notre compréhension des langages de programmation.
La Complexité de la Complétude de Turing en C
Introduction
La question de savoir si le langage de programmation C est Turing-complet suscite des débats parmi les informaticiens. Bien que des discussions aient eu lieu dans le passé, il semble que la réponse soit négative pour des raisons assez subtiles.
Simulation d’une Machine de Turing
Dans la plupart des langages de programmation, il est possible de simuler une machine de Turing. Cela peut être réalisé par :
- La simulation d’un automate fini à l’aide d’un programme utilisant une quantité limitée de mémoire.
- La représentation de la bande par une paire de listes chaînées d’entiers, qui symbolisent le contenu de la bande avant et après la position actuelle. Déplacer le pointeur implique de transférer la tête d’une liste à l’autre.
Bien qu’une implémentation concrète sur un ordinateur puisse manquer de mémoire si la bande devient trop longue, une version idéale pourrait exécuter le programme de la machine de Turing de manière fidèle. Cela pourrait être réalisé avec du papier et un stylo, ou en utilisant un ordinateur doté de plus de mémoire et un compilateur adapté à une architecture avec une plus grande taille de mot.
Limitations de C
Cependant, cette approche ne fonctionne pas avec le langage C, car il est impossible d’avoir une liste chaînée qui puisse croître indéfiniment : il existe toujours une limite au nombre de nœuds.
Comprendre l’Implémentation en C
Pour saisir pourquoi cela est le cas, il est essentiel de comprendre ce qu’est une implémentation en C. C est en réalité une famille de langages de programmation. La norme ISO C définit la syntaxe et la sémantique de cette famille de langages. C présente de nombreux comportements indéfinis et des comportements définis par l’implémentation. Chaque implémentation de C représente un langage distinct, et le terme « implémentation » désigne en fait une variante de langage.
Dans une implémentation donnée de C, un octet peut avoir $2^{texttt{CHAR_BIT}}$ valeurs possibles. Toutes les données peuvent être représentées sous forme de tableau d’octets : un type t a au maximum $2^{texttt{CHAR_BIT} times texttt{sizeof(t)}}$ valeurs possibles. Ce nombre varie selon les implémentations, mais pour une implémentation donnée, il reste constant.
Limites des Pointeurs
En particulier, les pointeurs peuvent prendre au maximum $2^{texttt{CHAR_BIT} times texttt{sizeof(void)}}$ valeurs. Cela signifie qu’il existe un nombre maximum d’objets adressables. Les valeurs de CHAR_BIT et sizeof(void) sont observables, donc si vous manquez de mémoire, vous ne pouvez pas simplement relancer votre programme avec des valeurs plus grandes pour ces paramètres. Vous exécuteriez le programme sous un langage de programmation différent — une autre implémentation de C.
État Limité des Programmes
Si les programmes d’un langage ne peuvent avoir qu’un nombre limité d’états, alors ce langage n’est pas plus expressif que les automates finis. La partie de C qui est limitée au stockage adressable ne permet au maximum que $n times 2^{texttt{CHAR_BIT} times texttt{sizeof(void*)}}$ états de programme, où $n$ est la taille de l’arbre de syntaxe abstraite du programme. Par conséquent, ce programme peut être simulé par un automate fini avec ce nombre d’états. Si C est plus expressif, cela doit passer par l’utilisation d’autres fonctionnalités.
Profondeur de Récursion
C n’impose pas directement une profondeur de récursion maximale. Une implémentation peut en avoir une, mais elle peut aussi ne pas en avoir. Cependant, comment communiquer entre un appel de fonction et son parent ? Les arguments ne sont pas utiles s’ils sont adressables, car cela limiterait indirectement la profondeur de récursion. Par exemple, si vous avez une fonction int f(int x) { … f(…) …}, toutes les occurrences de x dans les frames actives de f ont leur propre adresse, et donc le nombre d’appels imbriqués est limité par le nombre d’adresses possibles pour x.
Utilisation de Stockage Non-Adressable
Un programme C peut utiliser un stockage non-adressable sous la forme de variables register. Les implémentations « normales » ne peuvent avoir qu’un nombre limité de variables sans adresse, mais en théorie, une implémentation pourrait permettre une quantité illimitée de stockage register. Dans une telle implémentation, vous pourriez effectuer un nombre illimité d’appels récursifs à une fonction, tant que ses arguments sont register. Cependant, comme les arguments sont register, vous ne pouvez pas créer de pointeur vers eux, ce qui nécessite de copier explicitement leurs données : vous ne pouvez passer qu’une quantité finie de données, et non une structure de données de taille arbitraire composée de pointeurs.
Conclusion
Avec une profondeur de récursion illimitée et la restriction selon laquelle une fonction ne peut obtenir des données que de son appelant direct (arguments register) et renvoyer des données à son appelant direct (valeur de retour de la fonction), vous obtenez la puissance des automates à pile déterministes.
Il est difficile de trouver une manière d’aller plus loin dans cette discussion. Bien sûr, il serait possible de stocker le contenu de la bande à l’extérieur, via des fonctions d’entrée/sortie de fichiers. Mais cela soulèverait une question différente : celle de savoir si C, associé à un système de stockage infini, est Turing-complet, à laquelle la réponse serait un ennuyeux « oui ».
Général
Le pare-brise de la BMW Panoramic iDrive : une expérience immersive à couper le souffle !
BMW a révélé son nouveau système Panoramic iDrive, révolutionnant l’expérience de conduite avec un affichage tête haute 3D qui s’étend sur tout le pare-brise. Imaginez un intérieur où toutes les informations essentielles, comme la vitesse et les directions, sont projetées directement dans votre champ de vision ! C’est une véritable couche de réalité augmentée qui connecte le conducteur à la route.
Avec des boutons haptiques sur le volant et un écran tactile central innovant, chaque détail est conçu pour une personnalisation optimale. Préparez-vous à découvrir cette technologie futuriste dans le prochain SUV électrique X-Class de BMW fin 2025 !
Une Révolution Technologique : Le Nouveau Système BMW : un aperçu captivant du futur de l'infodivertissement »>iDrive Panoramique de BMW
une Vision d’Avenir
BMW a récemment présenté son innovant système iDrive Panoramique,qui se distingue par un affichage tête haute en 3D impressionnant,occupant l’intégralité du pare-brise. si vous pensiez que l’intérieur épuré des Tesla était à la pointe, attendez de découvrir cette nouvelle approche.
Un Affichage Révolutionnaire
Fini le tableau de bord traditionnel devant le volant. Désormais, toutes les informations sont projetées directement dans le champ de vision du conducteur via le pare-brise. Cela inclut la vitesse, les données d’assistance à la conduite, les feux de circulation, les panneaux routiers et même des indications de navigation et niveaux de batterie. Chaque élément est personnalisable pour que chaque conducteur puisse choisir ce qu’il souhaite afficher. Par exemple, lorsque l’assistance au conducteur est activée, le chemin navigué s’illumine en vert.
Frank Weber, directeur technique chez BMW, décrit cette configuration comme une couche de réalité augmentée qui maintient le conducteur connecté à la route.
Intégration des Retours Clients
La société a déclaré que l’intégration des instructions de navigation avec les données d’assistance au conducteur représente une évolution naturelle alors que nous nous dirigeons vers des niveaux plus élevés d’automatisation dans la conduite.De plus, ils ont souligné que les retours clients ont été essentiels pour façonner plusieurs fonctionnalités intelligentes affichées sur ce nouveau système.
Un Volant Repensé
Les innovations ne s’arrêtent pas au pare-brise ; BMW a également repensé son volant en y intégrant des boutons haptiques qui s’illuminent selon différents réglages.
Un nouvel écran tactile central en forme de losange accompagne cet interface sur le pare-brise et permet aux utilisateurs d’interagir directement avec lui.Ce dernier offre une interface hautement personnalisable où chacun peut prioriser ses applications favorites (appelées « pixels » par BMW) pour un accès rapide et facile. La marque envisage également un magasin d’applications pour encore plus de fonctionnalités et personnalisations.
Un Système opérationnel Innovant
Le logiciel qui alimente ce système est appelé BMW Operating System X ; il est développé entièrement en interne par l’entreprise et repose sur Android Open Source Project.
L’Intelligence Artificielle au Service du Conducteur
Aucun lancement technologique en 2025 ne serait complet sans une touche d’intelligence artificielle (IA).Le système iDrive utilise cette technologie pour apprendre les habitudes et comportements des conducteurs afin d’afficher automatiquement les applications pertinentes ainsi que leurs réglages préférés. Par exemple, si un utilisateur emprunte souvent un itinéraire spécifique vers son domicile tout en activant le mode sport, ces paramètres seront proposés proactivement lors du prochain trajet.De plus, selon BMW ,les modèles linguistiques avancés rendent les commandes vocales beaucoup plus naturelles et conversationnelles ; plutôt que d’utiliser des mots-clés spécifiques comme « station », il suffit simplement aux conducteurs dire quelque chose comme « trouve une station de recharge près du supermarché ».
Début D’une Nouvelle Ère
Ce design intérieur audacieux fera ses débuts dans le futur SUV électrique X-Class prévu fin 2025; plusieurs autres véhicules basés sur la nouvelle plateforme « Neue Klasse » suivront bientôt après cela.
Considérations Sécuritaires Émergentes
Un changement aussi radical pourrait diviser l’opinion parmi ceux attachés aux intérieurs classiques dotés depuis longtemps d’aiguilles traditionnelles et compteurs analogiques caractéristiques chez BMW . Il sera également intéressant d’observer comment la marque abordera les préoccupations relatives à la sécurité; celles-ci étant devenues cruciales pour toutes entreprises automobiles électriques adoptant entièrement interfaces tactiles . En effet , Euro NCAP introduira dès 2026 nouvelles directives exigeant certaines fonctions essentielles soient accessibles via boutons physiques afin qu’un véhicule puisse obtenir cinq étoiles lors évaluations sécurité .
Général
Nvidia révolutionne le monde physique avec GenAI et Cosmos !
Lors de la keynote très attendue du CES 2025, le PDG de Nvidia, Jensen Huang, a captivé l’audience avec des annonces révolutionnaires. Parmi les innovations présentées, le modèle Cosmos se distingue par sa capacité à transformer l’IA générative en actions physiques. Cela signifie que des robots et véhicules autonomes pourront réagir plus efficacement aux stimuli du monde réel. Nvidia ouvre ainsi la voie à une nouvelle ère d’applications robotiques et automobiles, tout en rendant ses modèles disponibles gratuitement pour encourager l’expérimentation.
Innovations Technologiques : les Annonces Marquantes de Nvidia au CES 2025
Un Événement Incontournable
Lors du CES 2025, l’une des conférences les plus attendues a été celle de Jensen Huang, le PDG de Nvidia. Ce dernier a présenté une série d’annonces captivantes touchant à divers sujets technologiques d’actualité tels que l’intelligence artificielle (IA), la robotique et les véhicules autonomes.
Nouveaux Produits et Progrès Technologiques
Vêtu d’une version scintillante de son emblématique blouson en cuir noir,Huang a détaillé les dernières cartes graphiques GeForce RTX 50 ainsi que des modèles fondamentaux d’IA appelés Nemotron. Il a également partagé des plans pour des agents alimentés par IA.
Parmi les innovations notables figurent des extensions à la plateforme Omniverse, qui permet la création de jumeaux numériques et simule l’interaction entre l’IA et le monde physique. De plus, un superordinateur AI compact nommé Project Digits a été introduit, propulsé par le GPU Grace Blackwell.
Cosmos : Une Révolution dans l’Intelligence Artificielle
Une annonce particulièrement intrigante fut celle du projet Cosmos. Ce dernier est défini comme un ensemble complet de modèles fondamentaux mondiaux intégrant des tokenizers avancés et une pipeline vidéo sophistiquée.L’objectif principal est d’étendre les capacités génératives de l’IA au-delà du numérique vers le monde physique.
En termes simples, alors que la plupart des systèmes génératifs se concentrent sur la création numérique basée sur une vaste base documentaire ou visuelle, Cosmos vise à produire des actions physiques en s’appuyant sur ses données issues d’environnements simulés numériquement.
Implications pratiques pour Divers secteurs
Les implications pratiques sont significatives pour divers domaines tels que la robotique ou les véhicules autonomes. Par exemple, grâce à Cosmos, il devient possible pour un robot humanoïde d’apprendre à exécuter efficacement une tâche spécifique comme retourner une omelette ou manipuler des pièces dans une chaîne de production.De même,un véhicule autonome peut s’adapter dynamiquement aux différentes situations rencontrées sur la route.
Actuellement,ces formations reposent souvent sur un travail manuel intensif où il faut filmer plusieurs fois chaque action humaine ou faire parcourir aux voitures autonomes plusieurs millions de kilomètres. Avec Cosmos cependant,ces méthodes peuvent être automatisées ce qui réduit considérablement coûts et délais tout en élargissant le volume de données disponibles pour entraîner ces systèmes.
La Plateforme cosmo : Un Outil Puissant
Nvidia présente donc Cosmos comme une plateforme dédiée au développement mondial fondée sur l’IA générative qui intègre divers outils facilitant cette évolution technologique rapide. En tant qu’extension directe du simulateur Omniverse déjà existant chez Nvidia, elle permet non seulement d’extrapoler les modèles numériques mais aussi leur request concrète dans notre réalité quotidienne.
Au cœur même du projet se trouvent ces modèles fondamentaux construits grâce à millions heures vidéos accumulées permettant ainsi aux machines formées avec cette technologie réagir avec précision face aux stimuli physiques variés qu’elles rencontrent dans leur environnement réel.
Vers un Avenir Prometteur
Jensen Huang n’a pas manqué souligner lors sa présentation comment nous assistons actuellement à une transition majeure vers ce qu’il appelle « l’IA physique ». en rendant ses modèles disponibles gratuitement afin encourager recherche avancée en robotique et véhicules autonomes , Nvidia montre sa volonté soutenir innovation tout en anticipant tendances futures .
À court terme cependant , cet impact pourrait rester limité car principalement destiné développeurs spécialisés . Néanmoins , son potentiel transformationnel pourrait accélérer considérablement progrès produits concernés tout en améliorant sécurité efficacité systèmes associés .Ces développements témoignent également transformation continue chez Nvidia vers entreprise axée logiciel capable bâtir plateformes adaptées nouvelles applications émergentes. Pour ceux intéressés comprendre direction future société , ces annonces offrent perspectives fascinantes quant maintien croissance impressionnante entreprise .
Général
L’écran tactile secondaire Corsair Xeneon Edge : un 32:9 qui s’installe partout !
Qu’est-ce qui vient de se passer ? Le CES est toujours une vitrine incroyable de produits technologiques, et cette année, Corsair nous surprend avec son écran tactile Xeneon Edge. Avec ses 14,5 pouces et un rapport d’aspect 32:9, cet écran secondaire pourrait bien devenir l’outil indispensable pour les passionnés de technologie. Grâce à sa résolution impressionnante de 2560 par 720 pixels et à sa connectivité polyvalente via USB Type-C ou HDMI, il s’adapte à tous vos besoins. Imaginez pouvoir gérer vos réseaux sociaux tout en surveillant votre système ! Restez à l’affût pour plus d’infos !
Nouveaux Horizons Technologiques : Le Xeneon Edge de Corsair
Qu’est-ce qui se passe ?
Chaque année, le CES présente une multitude de nouveaux produits technologiques, certains étant plus pratiques que d’autres. L’intérêt que vous portez à l’écran tactile Xeneon Edge de Corsair dépendra probablement de votre besoin d’un écran secondaire de 14,5 pouces au format 32:9.
Une Évolution des Écrans Secondaires
Bien que les écrans secondaires ne soient pas une nouveauté, leur complexité a considérablement augmenté ces dernières années. Le Xeneon Edge se distingue par son design innovant et ses caractéristiques techniques impressionnantes. Avec une résolution LCD de 2560 x 720 pixels, il offre une densité d’affichage remarquable de 183 PPI, un niveau de luminosité atteignant 350 nits et un taux de rafraîchissement à 60 Hz sur son panneau IPS.
Flexibilité et Installation
Le Xeneon Edge est conçu pour s’adapter à divers environnements. Il peut être placé sur un bureau grâce au support inclus ou fixé à un PC ou toute surface ferromagnétique grâce aux quatorze aimants intégrés. De plus, il peut être installé dans un boîtier via un point de montage pour radiateur de 360 mm, ce qui est plutôt séduisant. Corsair affirme également qu’il est plus mince qu’un ventilateur classique, minimisant ainsi les préoccupations liées à l’espace.
Connectivité et Utilisation Pratique
Pour la connexion, le dispositif utilise soit le port USB Type-C DP-Alt Mode soit un port HDMI standard. Une caractéristique intéressante est sa capacité à fonctionner en orientation verticale ou horizontale.Cela en fait un outil idéal pour ceux qui souhaitent faire défiler leurs fils d’actualités sur les réseaux sociaux ou surveiller Discord simultanément. Windows reconnaîtra le Xeneon Edge comme écran additionnel.
Corsair indique également que cet écran tactile capacitif multi-touch à cinq points fonctionne comme n’importe quel autre affichage tactile sous Windows.!Fonctionnalités du Xeneon Edge
Intégration avec iCue
L’écran s’intègre parfaitement avec le logiciel iCue de Corsair permettant aux utilisateurs d’accéder facilement aux informations concernant la vitesse des ventilateurs du système, les températures ainsi que l’utilisation du CPU et GPU. Les utilisateurs peuvent aussi ajuster différents paramètres tels que les profils lumineux et la gestion des ventilateurs directement depuis l’écran tactile.
Disponibilité et Prix
Aucune details précise n’a encore été communiquée concernant le prix du xeneon Edge; cependant, il pourrait s’avérer assez onéreux compte tenu des fonctionnalités avancées proposées par cet appareil innovant. La disponibilité est prévue pour le deuxième trimestre 2025 chez les revendeurs Corsair ainsi que sur leur site officiel.
Dans cette même veine technologique, nous avons déjà vu plusieurs écrans LCD intégrés dans des systèmes AIO (All-in-One) refroidis par liquide auparavant; notamment celui proposé par Lamptron l’année dernière qui servait également d’écran secondaire ou encore Tryx qui a dévoilé en mars dernier ce qui était considéré comme le premier refroidisseur AIO doté d’un écran AMOLED incurvé.
-
Général5 mois agoX (anciennement Twitter) permet enfin de trier les réponses sur iPhone !
-
Technologie4 mois agoLe PDG de Broadcom anticipe la montée en puissance des hyperscalers avec des clusters d’un million d’accélérateurs !
-
Général4 mois agoL’Inter brille de mille feux face à Man City – Inzaghi enflamme le match !
-
Science et nature4 mois agoUne OLED révolutionnaire pour une vision nocturne compacte et légère !
-
Divertissement4 mois agoRésumé de l’épisode 2 de « Agatha All Along » : Plongée dans le monde des sorcières !
-
Général4 mois agoJáder Obrian marque à la 47e minute et propulse Austin FC en tête 1-0 face à LAFC !
-
Général4 mois agoL’interdiction de l’avortement en Géorgie a coûté la vie à une jeune mère : la droite chrétienne désigne désormais la victime comme coupable
-
Général4 mois agoLes scientifiques redéfinissent l’avenir scientifique de l’Afrique lors de la 15e conférence de l’AAS à Abuja